Arp Galaxies 1 to 50
Arp Galaxies 1 to 50
How Do We Measure Distances in Space?
As you stand and look at the sky and you see the multitude of twinkling lights, maybe you wonder just how do we know how far away they are from us? We will try to explain some of the ways this is done, starting with objects which are close to us and finishing as far out as we can go. The techniques used are sometimes simple, sometimes a little complicated, but we'll try to explain as simply as possible. It should first be mentioned that some of the more sophisticated techniques are always being refined as more and more is learned, and this causes fairly regular slight revisions to the estimated size of our Universe, as we shall see later.
Earthly Measurements
Since the earliest days man has used all sorts of things to measure distance. Personally, I have used pieces of paper with little marks on, and even knotted string to measure short distances, although a sophisticated piece of equipment called a ruler is normally better. When we measure a room for a carpet or for wallpaper, we often pace it out or perhaps use your feet end to end (my feet happen to measure about a foot – imagine that!). You might also have seen the men who walk along the side of the road pushing a wheel on a pole and wondered what they were doing. In fact, they are measuring distance. As the wheel turns this turns a cog wheel, which adds up the distance which the wheel has traveled, much along the lines of how the odometer on a car works. Well, that’s OK for a roadway, but you can’t push a wheel to the moon, and even if you could it would be tough to read the dial as you went, so different techniques have to be used when we reach for the planets and then the stars. Those techniques have to be more advanced to allow for the fact that you can’t always hold a tape measure to the object as you measure how far away it is.
The technique most commonly used for nearby objects, and one which is based on a procedure used for measuring distances on the earth for years, is called trigonometric parallax. It relies on a distant object appearing for the observer to be at a different place relative to the background, depending on where the observer is standing. This is perhaps best illustrated using a diagram.
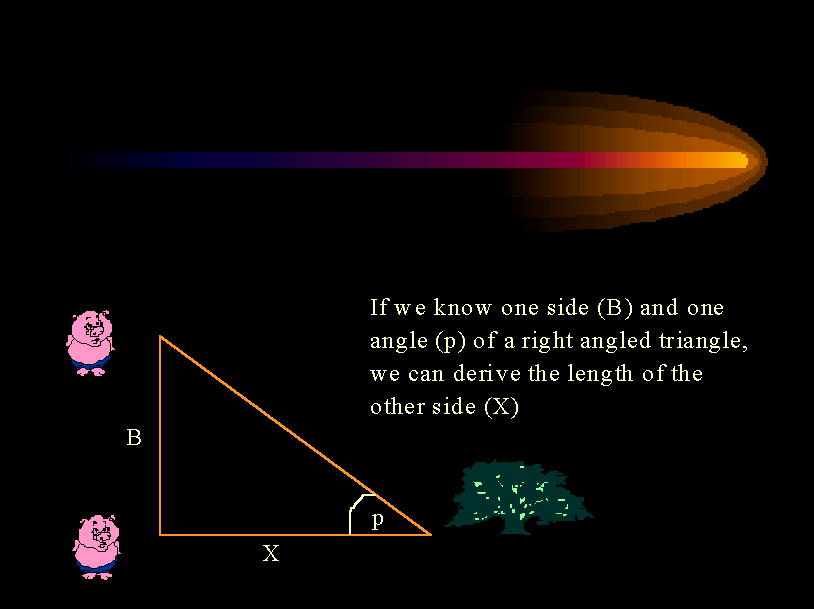
The way this works is that the observer sees the object (a tree in this case) when they are standing at the lower position. When they then move to the upper position, they sees the tree in a different position, and an angle (p) is created between position one and position two. Knowing how far apart are the two locations from which the observations have been made, and knowing the angle, it is possible to calculate the distance to the tree using simple trigonometry. Using this technique we can make very accurate distance determinations on the surface of the Earth. The interesting thing is that trigonometric parallax also works well for the planets and the nearer stars, but as the objects get further and further away from us the angle p becomes very small, and there can be large errors of measurement. Somehow we have to increase the length of the base line (B). But we can only use two points which are as far apart on the Earth’s surface as possible - can’t we?. Well, actually no. There is a way around our problem!
Extending the Baseline
The question posed is, "How can we extend the baseline for our measurements beyond the diameter of the Earth, without falling off the edge?". Well, what we do is to take a picture of the object - maybe a star or a planet - against the background of all the other stars. We then take another picture of the same object six months later, by which time the Earth has moved to the other side of its orbit around the sun. In this way we can use the diameter of the Earth’s orbit around the sun for our baseline, which is about 300 million kilometres, and this gives us a much larger angle to measure. Because we know the diameter of the Earth’s orbit, and also have measured the angle between the object’s apparent position at points on opposite sides of the orbit, we can calculate the distance to the object using simple trigonometry. This procedure uses the phenomenon called "parallax". On a point of astronomy, if the object is a nearby star and if the shift angle is 1 arc second then the star’s distance from us is 3.26 light years, and this is defined as a PARSEC (Which is actually shorthand for a Parallax Second). Parsecs are used to measure intergalactic distances, as we shall see. To put this all in perspective the tip of a ball point pen subtends an angle of 1 second of arc if viewed from across a football field. Using this technique we can measure, from the Earth, angles as small as 1/50 arc seconds which means that we can measure distances for stars which are up to 50 parsecs away. In fact, when measuring from the surface of the Earth this method only covers about a thousand of the nearest stars. However, we can further refine the technique by using measurements made from outside of Earth’s interfering atmosphere. The Hubble Space Telescope is not the only optical device which has been placed outside of our atmosphere. The Hipparcos star charting mission enabled us to make very precise measurements of star angles, and this increased significantly the number of local stars for which a precise position and distance is known. This enabled us to use the procedure out as far as 100 parsecs. But there comes a point at which our ability to make these sensitive measurements becomes inadequate, and we are once again stuck. Or are we? Of course you know that we're not, and there are additional techniques available to us which we can use, as you'll see.
Beyond 100 Parsecs
The basis of one of the best of these additional techniques relies on the fact that we know in quite a bit of detail at which wavelength, and therefore "color" of a star, is the maximum intensity of its spectrum. This technique, which is called "spectroscopic parallax", is based on the Hertzsprung-Russell diagram, which relates absolute luminosity to spectral class for a star. Absolute luminosity, intrinsic brightness and absolute magnitude are basically the same thing and they are plotted on the vertical axis, while the spectral class for a star (OBAFGKM) which is temperature dependent, is plotted on the horizontal axis. What the diagram shows is that "main sequence" stars such as our Sun, are those which are evolving in a predictable way and are in the first phase of their evolution as they burn hydrogen in their cores, producing helium. More importantly their intrinsic brightness can be determined by finding first their temperature (and hence their spectral class) and then extrapolating in the H-R diagram.
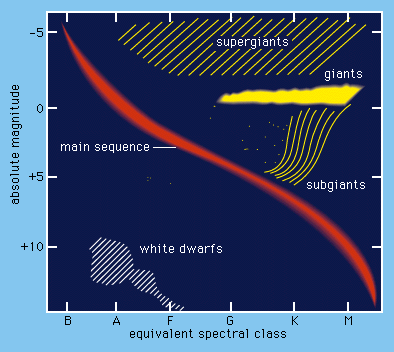
Now, you perhaps already know that a star’s observed brightness decreases with the square of the distance. If we measure the apparent brightness of a star and know its intrinsic brightness (how brightly is it actually shining), then we can calculate how far away it is. This technique works out to distances of about 50,000 parsecs, which is about twice the diameter of our own Milky Way galaxy. So now we are really getting out there, but the limited value of this new tool is obvious if we look at the distance to our nearest large neighbor galaxy, Messier 31 in the constellation of Andromeda. This large galaxy, part of what is know as the "local group of galaxies" and one of our nearest neighbours is 675,000 parsecs away from us, and so we have to develop totally new techniques if we are to measure the distance, not just to galaxies of our local group, but also to other galaxies which are much more remote.
Beyond Andromeda
The first step in this procedure is to use the luminosity of bright features which we can recognize in galaxies. In this we are quite lucky, because of the discovery of two particular types of star which vary in brightness in very predictable ways. These two types of special stars are called RR-Lyra stars and Cepheid variables. In both these cases the intrinsic luminosity of the star is closely linked to the period of variation in brightness. The Cepheids are also particularly bright stars, and so they are visible over great distances. If we can observe a Cepheid in another galaxy, and if we can determine its intrinsic brightness, then we can apply the inverse square law as before to calculate its distance from us. So, with Cepheids all we have to do is measure the period of variation in brightness which, as we have learned establishes the intrinsic brightness, and we can determine how far away it is from us. It turns out that Cepheids can be seen in nearby galaxies, and so using this procedure it has been possible to measure distances out as far as 150 million parsecs, which takes in quite a few galaxies. As we start to use Hubble and the new very large telescopes to image Cepheids in ever more distant galaxies we can make much more accurate measurements of distances out through 300 million parsecs and more. But what about even greater distances?
The Final Step
The first thing we do when taking that next step "out there" is to use the Cepheid variable and other techniques to measure as accurately as we can the distances to nearby galaxies. We can also measure the overall apparent luminosity for those galaxies. If we then compare the type of galaxy whose parameters we have measured accurately, with similar galaxies which are a lot further away, then estimates can be made of the distance of those remote galaxies, based on their apparent luminosity and angular diameter. In this process we again use the inverse square law, which determines the relationship between distance and apparent luminosity. But this technique relies heavily on the assumption that similar galaxies always have similar overall luminosities, and so we have to be careful when we use this procedure.
Another technique now also comes into play. You know how, when an emergency vehicle comes towards you with its siren going the sound appears to fall in tone as the vehicle passes you? Well, this is called the Doppler effect, and it is caused because the sound waves are compressed as the car approaches you, making the sound appear to be of a higher frequency (hence, a higher pitch), and as the car passes you and moves away the sound waves are stretched, making the sound appear to be of a lower frequency (lower pitch).

Now, due to the fact that light – at least for some of the time (and we won’t go down that road today!) – behaves as if it were a wave with a wavelength, then the same type of Doppler effect can be observed with light. Light from objects which are moving towards us is "compressed" to a shorter wavelength, turning it bluer than it should be, and that from objects traveling away from us is "stretched" to a longer wavelength, turning it redder than it should be. What we find when we look at light received from most galaxies away from our local group, is that their light is reddened, which means that they are receding from us. We determine this by analyzing their spectra, when we can see that the place where we expect to see certain spectral lines is shifted towards the red end of the chart. In 1929 the American astronomer Edwin Hubble realized that not only did other galaxies appear to be moving away from our Milky Way galaxy, but the farther away they are the faster they appear to be moving. And so was born the "Hubble Constant" – H0. The Hubble Constant is a number which relates a galaxy’s apparent speed of recession to its distance from the Milky Way galaxy. It is normally expressed in units of "Kilometers per second per Megaparsec", with a Megaparsec being about 3.26 million light years. So, what the Hubble constant tells you is that for every 3.26 million light years you look out into space the objects there appear to be receding from you at a rate of H0 kilometers per second. Or, put another way, if H0 is 100 then the objects appear to recede at a rate of 100Km/second for every 3.26 million light years you look out into space, but if H0 is only 50, then you have to look about 6.52 million light years out into space before you see the same 100 Km/second recessional velocity. If you like formulae, then the applicable one here is Speed of recession = H0 x distance (where H0 is the Hubble Constant). You can see therefore that determining the value of the Hubble Constant is quite important if we are to be able to accurately measure the size of the universe. It turns out that it is particularly difficult to obtain an accurate value for H0 and numbers between 50 and 100 have historically been proposed. But as techniques have become more and more refined it has been possible to reconcile these conflicting findings, and a value for the Hubble constant of about 65 or 70 now seems to be gaining ground as the agreed value. A final, interesting fact is that, if we look at the units in our equation v = H0 x distance, then we have Km x sec-1 = Constant x Km. The kilometers cancel out both sides to leave the reciprocal of H0 as seconds, meaning that the good old Hubble constant gives us a direct measure of the age of the Universe. The currently accepted number of 70 for H0 agrees well with the calculated oldest possible age for the universe as measured by other means, such as by estimating the ages of the oldest known stars in globular clusters. This whole subject is another very interesting area – but is not one I propose to cover in this discussion!
So, it’s been a long, long journey, from our little pink pig and the parallax measurements at the beginning of this story, to measurements at the beginning – or end, which is it – of time. I hope you have enjoyed making this journey with us and that now you have at least a fair understanding of how astronomers measure distance.