Arp Galaxies 1 to 50
Arp Galaxies 1 to 50
Celestial Coordinates
People always seem to have great difficulty understanding celestial coordinates. So this section is dedicated to giving you an understanding of how astronomers describe where a celestial object is in the sky. But first it is important to understand geographical coordinates, or how we identify where exactly a place is located on the surface of planet Earth. Everyone knows that the Earth turns on its axis, and that mid-way between the north and south poles is an imaginary line which we draw around the world, called the Equator. We can also draw other imaginary lines around the world, all equally spaced, and we call these lines, lines of latitude. We give the equator a latitude of zero degrees, and the poles - because they are right angles to the equator - are therefore plus and minus 90 degrees, as shown in this diagram.

So this gives us a method for describing to someone how far north or south a place is on the surface of the Earth. We simply give it a latitude in degrees. To make the location more accurate we divide the degrees up into minutes (60 minutes per degree) and we can further refine our measurement by dividing the minutes up into seconds (60 seconds in every minute). Now we know pretty accurately how far north or south our location is, but we also need to know how far east or west it is. If we know how far east or west, then we can describe any location very precisely. To achieve this we draw another series of imaginary lines (remember that none of these lines is actually drawn on the Earth's surface) from north pole to south pole. Again we space the lines equally all around the planet, and we call these lines lines of longitude. This time we don't have a convenient "centre" or equator, and so international convention has adopted the line of longitude which passes through Greenwich, England as being the line of zero longitude. The lines are marked going east of Greenwich and west of Greenwich, so we can have longitudes up to 180 degrees east or 180 degrees west.
And now we're ready to make the jump to celestial coordinates!
Let's start by imagining something the ancients believed - that the sky is actually a fixed sphere, and the stars and planets are points on this sphere. Although we now know that this is not true, for the purposes of describing where an object can be found in the sky it is quite adequate. Next, imagine the lines of latitude and longitude being extended outwards from the surface of the Earth until they touch this sphere. Those of you with a good imagination can now visualise lines painted on the sky, with the lines of latitude running from east to west around the sky, and lines of longitude running north to south, radiating away from the celestial pole. So where's the celestial pole? It's simply the point in the sky to which the north or south pole of Earth points. Or put another way, if you stuck a skewer through the turning axis of the Earth, one end would be at the north celestial pole and the end at the south. For those of you still having trouble, here is another diagram:
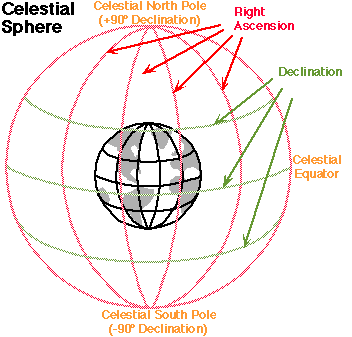
And now we are getting close to being able to describe the location of a celestial object. You can see from the diagram that the lines of latitude in astronomy are called lines of declination. They are divided into degrees, minutes and seconds exactly as they are on the Earth's surface, and so by quoting the declination of an object in degrees, minutes and seconds we can describe exactly how far "north or south" it is from the celestial equator. It might help if we add here that the celestial equator normally draws an arc across the night sky, with a maximum "height" above the horizon equal to the latitude of where you are on the Earth. That only leaves us with the "longitude" or how far east or west something is. As you might expect, the lines of longitude are not called that in astronomy, and another confusing factor is that we do not measure them in degrees like we do everything else up to now. Because the Earth is divided into 24 one hour "time zones" running east to west and west to east, we use hours, minutes and seconds for this measurement, and we call the measurement the right ascension of an object. But as long as you remember that it's just another way of dividing up the available sky, you shouldn't be too confused. So to take a real life example, the star Vega has celestial coordinates of:
right ascension 18hours 36minutes 56seconds
declination +38degrees 47minutes 1second
This method of expressing coordinates allows us to point our telescope very precisely at Vega, or indeed at any other object in the sky.
Precession
So is that all there is to it? Well of course the answer is no. There is one significant complicating factor of which we need to be aware when identifying with any degree of certainty where an object can be found in the sky, and that is the precession of Earth's poles as the planet turns. It's time to start imagining again! We know something else about the Earth - we know that it is not turning upright with respect to the plane of the solar system (what we call the ecliptic), it is tilted at an angle of about 23 degrees. We also know that it we take a child's spinning top and start it spinning at an angle to the table on which it sits, it's spin axis will slowly circle around the upward direction of the force which the table applies to it - effectively the top will "wobble". This is a phenomenon known as precession. In exactly the same manner as our top, the spinning Earth slowly precesses because of the force which the tidal gravitational pull of the Moon and Sun on the slight equatorial bulge. This precession has quite a startling effect on our celestial coordinate system, because it causes the location of the celestial pole to vary as the north or south pole of the Earth point to different places in the sky. So how significant is this effect? Well, over a long period of time it can be pretty significant. The celestial pole moves around the sky in a full circle in about 26,000 years. Right now Polaris is our "pole star" in the northern hemisphere, but in 12,000 years time it will be Vega, which if you will recall from earlier in this section is currently at a declination of 38 degrees, not 90 degrees. So the changes are large, but the rate of change is slow. However, when we are describing the location of very small objects and are measuring down to seconds of arc, these changes are measurable and so we must specify the date for which a given measurement in right ascension and declination applies. The current standard is known as Epoch 2000.0 which is shorthand for "right ascension and declination at the moment the year 2000 begins". The previous standard was 1950.0. The celestial coordinates work very well for the stars and galaxies, which are sufficiently remote that they show no appreciable real movement from one year to the next. For objects like the sun and planets which move quite quickly across the sky, we often give coordinates for "equinox of date" - i.e. they are correct for the date on which they were issued. And finally, how much do we need to worry about this, will it affect my star charts and my backyard astronomy and my ability to find objects in the sky? Well, right now the answer is no, because from 1950 to 2000 the coordinate grid only moved across the sky by 0.7 degrees at the ecliptic - less than one field of view in a low powered telescope. We have also entered a new epoch and all our star charts will be right up to date. But as the years go by it will be necessary for advanced amateurs who have tracking and guiding equipment to make changes to their calculations, their polar alignment scopes and their star charts.